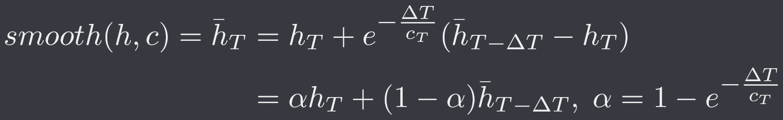Exponential Idle Basics
This guide is currently undergoing change. Keep in mind, strategies may change.
Table of contents
This intro and following guide are designed to help you play through the 1 to ee2000 section of the game. This introduction will give you some fundamentals to help you progress while playing this section of the game.
If you don’t want to have spoilers for the later game, don’t read further ahead than you are already.
Variables and Upgrades #
- Variables are the main purchases in the game. They will be the most important to buy, and you should buy them as priority because they increase Lifetime f(t) faster. All of the variables purchasable are below. You will not be able to get all of them right away but will be able to get them all as you keep playing. This screen is found by pressing the <Upgrades> button between the upgrades and the main equation graph.
- Upgrades are where additional boosts to variables lie. They are crucial to progress and should be bought often. You will be able to see items that can be purchased with f(t), \(\mu\), and \(\psi\) on that page in that order. You can navigate to that tab by pressing the <Variables> button between the variables and the main equation graph.
Variable Names #
| Name | Name | |||
|---|---|---|---|---|
| x | x | ν | nu | |
| y | y | ε | epsilon | |
| z | z | ζ | zeta | |
| s | s | η | eta | |
| u | u | θ | theta | |
| v | v | ι | iota | |
| w | w | ξ | xi | |
| α | alpha | μ | mu | |
| β | beta | ψ | psi | |
| γ | gamma | τ | tau | |
| δ | delta | φ | phi | |
| κ | kappa | σ | sigma | |
| λ | lambda | ρ | rho |
What does ee mean? #
You start out with normal numbers and quickly work your way up to \(X.xxeX\) notation. This notation is scientific notation. It stands for \(X.xx*10^X\). Later you are introduced to \(X.xxeeX\). This is a custom game notation that stands for \(X.xx*10^{10^X}\).
Achievements and Minigames #
- Achievements are just that. They are goals to reach that give you stars as reward.
- Minigames are puzzles that you can solve that will give you stars as a rewatd for getting solving them. Check out the Minigame Guide for how to solve each puzzle and more resources.
Stars and Star upgrades #
- Stars are a currency that opperates outside of the main game that you use to purchase star upgrades. These upgrades range from QoL features to boosts to the gameplay. For the most part, you should prioritize new variables as soon as you can, EXCEPT for Autoprestige. Autoprestige is a huge boost in power, and you should prioritize that over variables of a similar cost. More details on star upgrades to prioritize can be found in following guides.
Autoprestige expression #
timer(d(ln(db/b+1)/pt) < 0)
> 3 * tr && db > b
Autoprestige explanation #
The idea behind \(d(ln(db/b+1)/pt) < 0\) is clearer if you consider a different term \(d((db/b+1)^{(1/pt)}) < 0\). They measure the same thing, but the second one is just raised to the exponent, base e. They are equivalent because \(e^x\) (and \(ln (x)\)) are both strictly increasing functions on the domain \(x > 0\), so applying those functions will not change where the local maximum is located (when \(d\) changes sign).
\(db/b+1\) is better explained with \((b + db)/b\). \(b + db\) is the new \(b\) value you would get after prestige, and \(b\) is the old \(b\) value you currently have. If you prestige, your \(b\) is multiplied by that exact value. That is, your \(b\) grows with ratio \((b + db)/b\) if you were to prestige.
The general idea of a good expression would be to “maximize \(f\) growth over time,” and it would be the same as “maximize \(b\) growth over time.” To measure \(b\) growth over time, in this approach we take the growth of \(b\) that can result from current prestige only and take \((b + db)/b\) as the ratio of growth.
We could divide the ratio by time, but that doesn’t make sense because ratios are applied multiplicatively (e.g. ratio \(r\) per second means \(r^5\) in \(5\) seconds, not \(5*r\)). Hence, instead of dividing, we take the power \(1/pt\) (\(pt\) being the time since prestige) to get the correct value of ratio.
Therefore, we get the expression \(((b + db)/b)^{(1/pt)}\) which represents “after last prestige, \(b\) grew by \(this\) \(ratio\) per second.” To maximize this value, we note that this value actually achieves one local maximum (by working through the behaviors of (\(f\) over time) so we may simply take a derivative (\(d\)) and see when it turns negative.
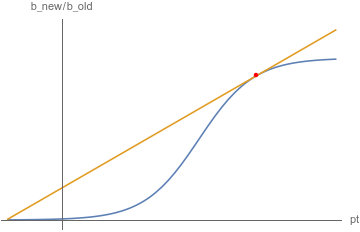
Visual representation #
Autosupremacy expression #
timer(d(ln(db / b + 1) / pt) < 0)
> 2 * tr && db > b && dpsi + psi
> min(min(costUpS(1), costUpS(2)), costUpS(3))
&& ln(1 + max(1, log10(sf)) /
smooth(max(1, log10(gf)), (st > tr) * ee99))
/ max(1, st) < smooth(ln(1 + max(1, log10(sf))
/ smooth(max(1, log10(gf)), (st > tr) * ee99)) /
max(1, st), (pt > tr) * ee99)
YOU NEED TO MANUALLY SUPREMACY WHEN YOU PUT THIS INTO YOUR GAME!
Reference Locking Smooth()
Autosupremacy explanantion #
The autosupremacy expression is an attempt to do the autoprestige expression, but for supremacy. It tracks the same information, but over multiple prestiges. It is harder to make an autosupremacy expression than an autoprestige expression because after a new prestige, Supremacy \(f(t)\) doesn’t increase until you get back to the \(f(t)\) you left off at. This creates the growth of a supremacy staircase shaped. This makes it difficult to find the optimal point as we did with autoprestige and is why we time it with the end of a prestige to be sure.
Smooth() for auto expressions #
Internally, smooth is implemented using exponential moving average. Here are some ways to use this construction.
Method 1: Moving average #
If a value fluctuates too much, you can use smooth so that the value does not go rampant, triggering some conditions incorrectly. One main example is to use it when you use multiple \(d()\) function on the same expression.
For instance, \(smooth( d(d(ln(db))), 10)\) will behave much better than the simple \(d(d(ln(db)))\) because using d multiple times creates a lot of fluctuation, due to the discrete nature of \(d()\) (not a true derivative, but an extrapolation of slope over the last tick). Of course, this introduces some “lag factor” in the sense that when some threshold is passed, smooth won’t display it until a short after.
Method 2: Lock #
Due to the nature of the expression, if the second input of smooth is very large, then there will be no average at all: instead of taking a normal average, we can skew the weights so that any new value is too small to be noticed. As a very simple example, can calculate averages like \(average = 0 * (new\) \( value) + 1 * (old\) \( value)\) to preserve old values. On the contrary, if we skew this the other way, then only the new value would appear: \(average = 1 * (new \) \(value) + 0 * (old\) \( value)\).
A simple expression like \(smooth(expr, ee99)\) will first compute expr and keep that value indefinitely until the expression field is reset: upon modifying the expression, every prestige for prestige expressions, and every supremacy for supremacy expressions. This is what we refer to as “lock.”
However, we can do better: instead of simply locking values, we can control when the locking mechanism comes in. Using conditions, we can switch back and forth between indefinite locks and instantaneous updates: \(smooth(expr, ee99 * cond)\). If cond is true, then \(ee99 * cond\) will be ee99, thereby activating the lock. If cond is false, then \(ee99 * cond\) will be 0, thereby switching to instantaneous updates. The result is that we obtain the value of expr evaluated when the cond was last false.
Method 3: Cumulative maximum #
If we have two really large values, the average of the two will be in favor of the larger of the two. In fact, if the two numbers are really really big, the average will be indistinguishable from the larger of the two due to finite data storage (term: floating point precision). We can abuse this idea to convert the input of smooth into a very large value, thereby converting averages like \(average = 0.5 * (new \) \(value) + 0.5 * (old\) \( value)\) into the equivalent \(average = max(new \) \(value, old \) \(value)\). The effect is that we obtain the maximum value that the input attained ever since the expression was reset (from modifying the expression or from prestige (resp. supremacy) for prestige expression (resp. supremacy expresssion)). Of course, we have to cancel out the magnification of the inputs in order to retrieve the value we actually want.
For example, \(smooth(10^{10^{10^{db}}}, 1)\) has the input large enough that it displays the largest value of \(10^{10^{10^{db}}}\) that occurred so far. However, we wouldn’t want db blown up this way, so we can use \(log_{10}(log_{10}(log_{10}(smooth(10^{10^{10^{db}}}, 1))))\) to retrieve back the maximum \(db\).
Reference formula #